Kreis und Flächeninhalt: Unterschied zwischen den Versionen
Gerard (Diskussion | Beiträge) K (Entfernte den Schutz von „Kreis; Flächeninhalt“) |
Gerard (Diskussion | Beiträge) K (Gerard verschob die Seite Kreis; Flächeninhalt nach Kreis und Flächeninhalt) |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Kreis Mittelpunkt Radius.jpg| | [[Datei:Kreis Mittelpunkt Radius.jpg|200px|links|Kreis mit Mittelpunkt M und radius]] | ||
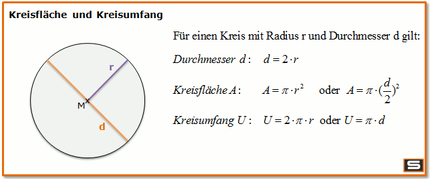
[[Datei:Kreisflaeche-kreisumfang-formel.png|430px|rechts|Flächeninhalt, Kreisumfang]] | |||
Ein [https://de.wikipedia.org/wiki/Kreis Kreis]<ref>[https://de.wikipedia.org/wiki/Kreis Wikipedia zu Kreis]</ref> ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises, er ist eine positive reelle Zahl. Der Kreis gehört zu den klassischen und grundlegenden Objekten der euklidischen Geometrie. | Ein [https://de.wikipedia.org/wiki/Kreis Kreis]<ref>[https://de.wikipedia.org/wiki/Kreis Wikipedia zu Kreis]</ref> ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises, er ist eine positive reelle Zahl. Der Kreis gehört zu den klassischen und grundlegenden Objekten der euklidischen Geometrie. | ||
Schon die alten Ägypter und Babylonier versuchten, den Flächeninhalt des Kreises näherungsweise zu bestimmen. Besonders in der griechischen Antike war der Kreis wegen seiner Vollkommenheit von großem Interesse. Beispielsweise versuchte Archimedes erfolglos, mit den Werkzeugen Zirkel und Lineal den Kreis in ein Quadrat mit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können. Ein solches Verfahren zur Berechnung des Flächeninhalts nennt man die Quadratur des Kreises. Erst 1882 konnte Ferdinand von Lindemann durch Nachweis einer besonderen Eigenschaft der Kreiszahl zeigen, dass diese Aufgabe unlösbar ist. | Schon die alten Ägypter und Babylonier versuchten, den Flächeninhalt des Kreises näherungsweise zu bestimmen. Besonders in der griechischen Antike war der Kreis wegen seiner Vollkommenheit von großem Interesse. Beispielsweise versuchte Archimedes erfolglos, mit den Werkzeugen Zirkel und Lineal den Kreis in ein Quadrat mit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können. Ein solches Verfahren zur Berechnung des Flächeninhalts nennt man die Quadratur des Kreises. Erst 1882 konnte Ferdinand von Lindemann durch Nachweis einer besonderen Eigenschaft der Kreiszahl zeigen, dass diese Aufgabe unlösbar ist. | ||
{{ClearLine}} | |||
== Quelle == | |||
<references /> | |||
[[Kategorie:Technologie]] | |||
[[Kategorie:Terranian Star Glossar]] | |||
Aktuelle Version vom 27. August 2023, 09:01 Uhr
Ein Kreis[1] ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises, er ist eine positive reelle Zahl. Der Kreis gehört zu den klassischen und grundlegenden Objekten der euklidischen Geometrie.
Schon die alten Ägypter und Babylonier versuchten, den Flächeninhalt des Kreises näherungsweise zu bestimmen. Besonders in der griechischen Antike war der Kreis wegen seiner Vollkommenheit von großem Interesse. Beispielsweise versuchte Archimedes erfolglos, mit den Werkzeugen Zirkel und Lineal den Kreis in ein Quadrat mit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können. Ein solches Verfahren zur Berechnung des Flächeninhalts nennt man die Quadratur des Kreises. Erst 1882 konnte Ferdinand von Lindemann durch Nachweis einer besonderen Eigenschaft der Kreiszahl zeigen, dass diese Aufgabe unlösbar ist.